|
На этой странице:
Компьютерная арифметика
Компьютерные числа
В основе компьютерной арифметики лежит двоичное кодирование.
Двоичное кодирование — это
кодирование информации при помощи нулей и единиц. Для компьютерных
технологий такой способ представления информации оказался очень
удобным.
Дело в том, что компьютеры построены на элементах, которые могут
находиться в двух возможных состояниях. Одно такое состояние обозначают
цифрой 0, другое — цифрой 1.
 Примером двоичного устройства служит обычная электрическая лампочка.
Она может находиться в одном из двух состояний: включена (состояние 1) или
выключена (состояние 0).
Примером двоичного устройства служит обычная электрическая лампочка.
Она может находиться в одном из двух состояний: включена (состояние 1) или
выключена (состояние 0).
Можно построить на лампочках электрическую память и хранить в ней
числа по цифрам при помощи такого кода:
| Двоичный код |
0-0000 |
1-0001 |
2-0010 |
3-0011 |
4-0100 |
| 5-0101 |
6-0110 |
7-0111 |
8-1000 |
9-1001 |
Видно, что для записи цифр от 0 до 7 хватило бы трёх лампочек, но ради двух
последних цифр (8 и 9) приходится под код цифры отводить четыре лампочки.
Вот так можно запомнить на лампочках число 6:

Установили переключатели в нужное положение — и пошли пить
чай! Если электричество не отключат, информация сохранится.
Электрические лампочки, конечно, не подходят для производства
компьютеров: они большие, быстро перегорают, дорого стоят (их ведь
нужны миллионы) и сильно нагревают окружающую среду.
В современных компьютерах в качестве элемента памяти используют
электронное устройство — транзистор.
Транзистор может пропускать через себя ток
(состояние 1) или нет (состояние 0).
 Было время, когда каждый транзистор изготовлялся отдельно и был
значительным по размеру.
Было время, когда каждый транзистор изготовлялся отдельно и был
значительным по размеру.
 Сейчас транзисторы, как и другие электронные элементы, изготовляют
способом, похожим на фотопечать, объединяя элементы в микросхему. В одной
микросхеме размером с ноготок может быть
“отпечатано” несколько миллионов транзисторов.
Сейчас транзисторы, как и другие электронные элементы, изготовляют
способом, похожим на фотопечать, объединяя элементы в микросхему. В одной
микросхеме размером с ноготок может быть
“отпечатано” несколько миллионов транзисторов.
Содержимое компьютерной памяти на микросхемах пропадает, как только
компьютер отключают от электрической сети. (В этом смысле транзистор
похож на электрическую лампочку!) Поэтому такая память используется
только для временного (оперативного) хранения и называется
ОЗУ (оперативное запоминающее устройство).
В качестве долговременной памяти используют магнитные носители
(винчестер, дискеты) и оптические — лазерные диски.
И на магнитных, и на лазерных дисках информация хранится также в двоичном
виде.
 Для записи информации на магнитный диск используют магнитные
свойства материала, из которого сделан диск: намагниченный участок
поверхности диска означает число 1, а ненамагниченный —
число 0.
Для записи информации на магнитный диск используют магнитные
свойства материала, из которого сделан диск: намагниченный участок
поверхности диска означает число 1, а ненамагниченный —
число 0.
 Комбинируя нули и единицы, можно закодировать любой знак, значит, на
диске можно записать и сохранить любую информацию.
Комбинируя нули и единицы, можно закодировать любой знак, значит, на
диске можно записать и сохранить любую информацию.
 Лазерные диски значительно превосходят магнитные дискеты по объёму: на
одном лазерном диске можно поместить информацию, записанную на сотнях
обычных дискет, тогда как по размерам они одинаковы.
Лазерные диски значительно превосходят магнитные дискеты по объёму: на
одном лазерном диске можно поместить информацию, записанную на сотнях
обычных дискет, тогда как по размерам они одинаковы.
 Информация на лазерный диск записывается в виде микроскопических
углублений на его поверхности. Яркость отражения лазерного луча
уменьшается, когда он попадает в углубления. Таким образом, удаётся хранить
и считывать информацию: углубление соответствует числу 0, а отсутствие
углубления — числу 1.
Информация на лазерный диск записывается в виде микроскопических
углублений на его поверхности. Яркость отражения лазерного луча
уменьшается, когда он попадает в углубления. Таким образом, удаётся хранить
и считывать информацию: углубление соответствует числу 0, а отсутствие
углубления — числу 1.
В компьютерной арифметике двоичный знак (0 или 1) называется битом.
Кратко эту единицу обозначают строчной буквой “б”.
Группа из 8 битов называется байтом (обозначается прописной
буквой “Б”). Можно написать формулу:
Более крупные единицы памяти:
| Килобайт (КБ) |
1 КБ = 1024 Б |
| Мегабайт (МБ) |
1 МБ = 1024 КБ |
| Гигабайт (ГБ) |
1 ГБ = 1024 МБ |
Позиционные системы счисления
Как понятно из вышеизложенного, в компьютерном деле популярна
двоичная система счисления.
Если в привычной десятичной системе для записи чисел используется
десять цифр (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), то в двоичной —
только две: 0 и 1.
Но обе эти системы счисления относятся к позиционным системам
счисления, то есть к таким, в которых значение числа
anan-1...a1a0,
составленного из базовых знаков (цифр ai)
определяется формулой:
N = anqn + an-1qn-1 + ... + a1q1 + a0q0 (*)
Здесь:
N — значение числа
q — основание системы счисления
ai — цифра системы счисления
В системе счисления по основанию q для представления чисел используется
q цифр. В десятичной системе (q=10) цифр десять, в двоичной
системе (q=2) — две.
Число 538 в десятичной системе счисления раскладывается по формуле
(*) так:
53810 = 5·102 + 3·101 + 8·100 = 5·100 + 3·10 + 8
Иными словами, младшая цифра означает единицы, вторая справа — десятки,
третья — сотни.
Та же запись 538 в 16-ричной системе счисления имеет совсем другое значение:
53816 = 5·162 + 3·161 + 8·160 = 133610
Обратите внимание: если в записи числа необходимо указать основание системы, то
основание приписывают справа от записи числа в виде подстрочного индекса.
Получается, что:
53816 = 133610
То есть запись 538 в шестнадцатеричной системе счисления означает то
же число, что и запись 1336 в десятичной системе.
А вот в двоичной системе запись 538 просто невозможна: числа
в двоичной системе счисления состоят только из нулей и единиц.
Формулу (*) удобно использовать для перевода числа из системы
счисления по основанию q в десятичную систему. Например, в
двоичной системе получим:
11012 = 1·23 + 1·22 + 0·21 + 1·20 = 8 + 4 + 0 + 1 = 1310
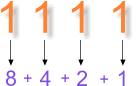 Единица в двоичном коде на нулевом месте справа дает число 1, на первом — 2,
на втором — 4, на третьем — 8.
Единица в двоичном коде на нулевом месте справа дает число 1, на первом — 2,
на втором — 4, на третьем — 8.
Вообще, единица на n месте справа (нумерация с нуля) означает 2n.
Перевод в десятичную систему счисления
Постановка задачи. Дана запись числа в системе счисления по основанию
q:
anan-1...a1a0,
Требуется. Найти значение этого числа в десятичной системе счисления
(перевести число в десятичную систему счисления).
Как решать. Решение основано на прямом использовании формулы (*):

Пример 1
Перевести в десятичную систему число 10112.
Решение
10112 = 1·23 + 0·22 + 1·21 + 1·20 = 8 + 0 + 2 + 1 = 1110
Замечание. При переводе из двоичной системы можно поступать так:
записать под каждой цифрой справа налево степени двойки по возрастанию
и выполнить сложение тех чисел, которые относятся к единицам двоичной записи:
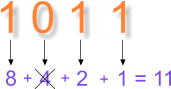
Пример 2
Перевести в десятичную систему число A2F316.
Замечание. В 16-ричной системе счисления — 16 цифр. Для обозначения
первых 10 используют десятичные цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Для
следующих шести — латинские буквы:
A — 10
B — 11
C — 12
D — 13
E — 14
F — 15
Решение
A2F316 = 10·163 + 2·162 + 15·161 + 3·160 =
= 10·4096 + 2·256 + 15·16 + 3 = 4171510
Перевод в q-ичную систему счисления
Перевод числа из 10-ой системы счисления в систему по основанию q основан на
той же базовой формуле (*):
N = anqn + an-1qn-1 + ... + a1q + a0 (*)
Заметим, что если поделить N на q, то в остатке получится
a0 — младшая цифра числа в системе счисления
по основанию q.
Целая часть от деления будет иметь вид:
anqn-1 + an-1qn-2 + ... + a2q + a1 (**)
Если поделить теперь на q число (**), то в остатке получим a1.
Продолжая работу в том же духе, можно последовательно получить все цифры
искомой записи числа в обратном порядке.
Пример 1
Перевести в двоичную систему число 25.
Решение
Делим число 25 на 2. Получаем 1 в остатке — это последняя цифра
двоичной записи.
Целую часть от предыдущего деления, число 12 снова делим на 2.
Получаем 0 в остатке — это вторая справа цифра
двоичной записи.
Продолжаем деление до тех пор, пока целая часть от деления не станет меньше
делителя — это первая цифра двоичной записи.
Процесс деления столбиком изображён на рисунке.
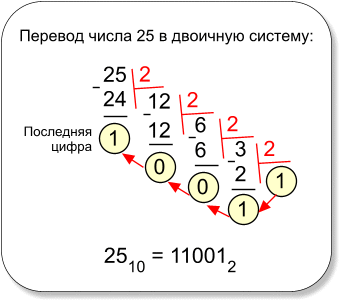
Ответ
2510 = 110012
Пример 2
Перевести в шестнадцатеричную систему число 3151.
Решение
Делим число 3151 на 16. Получаем 15 в остатке. Значит, последняя цифра
шестнадцатеричной записи равна F.
Целую часть от предыдущего деления, число 196 снова делим на 16.
Получаем 4 в остатке — это вторая справа цифра
шестнадцатеричной записи. Целая часть от последнего деления равна 12. Значит,
первая цифра искомой записи равна C.
Процесс деления столбиком изображён на рисунке.
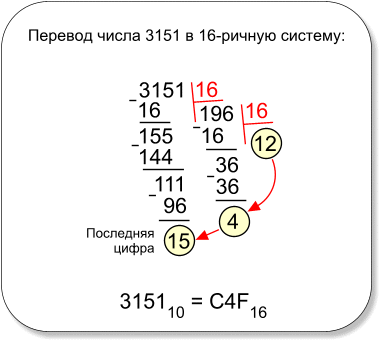
Ответ
315116 = C4F16

|

